Vaya, un tema que me gusta. Os vais a cagar.
Cuando era un joven y candoroso bachiller, una profesora de geografía que atesoraba un estremecedor caudal de incompetencia e ignorancia apareció cierto día por clase con un mapamundi en el que los contornos de los continentes se alejaban sensiblemente de las formas y proporciones a las que la mayoría estamos acostumbrados, mientras afirmaba rotundamente que
ése ─la proyección de Peters─ era el verdadero mapa del mundo, y que el mapa «de toda la vida» ─generalmente una proyección Mercator─ era poco menos que una burda conspiración del hemisferio norte para mantener en el más ignominioso subdesarrollo a los países del hemisferio sur a base de sobrerrepresentar el tamaño de aquéllos y disminuir el de éstos.
El mapa de marras:

Y aquí un ejempo de una proyección Mercator, que os sonará bastante más:

En aquella época era un mocoso y obviamente no tenía ni puta idea de nada, y aunque sospechaba que la buena mujer decía tonterías como puños, no sabía exactamente qué fallaba en su argumento. No fue hasta varios años después hasta que averigüé algo más sobre el tema.
El primer error es considerar una proyección
(1) «más correcta» que otra. El principal problema de los mapas es que nos empeñamos en «meter» algo esférico ─más o menos─ como es la Tierra dentro de un plano. Y claro, una esfera y un plano son muy distintos
(2), así que el ajuste no queda del todo bien, y hagamos lo que hagamos, el mapa siempre presentará algún tipo de distorsión. Lo único que nos queda es elegir qué queremos que se distorsione y qué queremos que reproduzca fielmente la realidad.
Concretando un poco, lo ideal sería que una proyección conservase las áreas de los continentes y sus formas
(3), aunque desgraciadamente, por lo que comentaba en el párrafo anterior, no existe ninguna proyección que cumpla ambas condiciones de manera simultánea, así que o bien elegimos una proyección que respete las formas pero distorsione las áreas (como la Mercator), o bien elegimos una que respete las áreas pero distorsione las formas (como la Peters) o bien una que no conserve ni área ni forma pero que haga que la distorsión sea razonable (por ejemplo, la proyección de Robinson).
Así pues, no se trata de que la proyección de Peters sea mejor o peor que la Mercator, simplemente que una pretende mantener las áreas mientras la otra se centra en conservar las formas.
De hecho, esto me lleva a otra de las cosas que me sorprendía cuando era crío: yo miraba los mapas y veía que Groenlandia aparecía con mayor tamaño que Australia, y me preguntaba por qué se consideraba que Australia era un continente y Groenlandia no. Mayor fue mi asombro al descubrir que, a pesar de su apariencia en los mapas, Australia casi cuadruplica el área de Groenlandia.
Esto se debe a que, como comentaba antes, la Mercator distorsiona las áreas, y la manera en que las distorsiona es haciendo los continentes más extensos conforme se alejan del ecuador.
Para ver mejor cómo funciona esta proyección, observad este dibujo:

La idea es rodear la esfera con un cilindro tangente al ecuador, proyectar cada punto de la esfera sobre el cilindro paralelamente al ecuador y desenrollar el cilindro. Como puede observarse, cerca del ecuador la superficie de la esfera y del cilindro no están muy distantes, por lo que la deformación es escasa, pero conforme nos acercamos a los polos, la distancia entre esfera y cilindro se incrementa, aumentando a su vez la distorsión, que se hace infinita en ambos polos.
Es por esto que, cuando se inventó esta proyección por el siglo XVI, tuvo tanto éxito, ya que los navegantes europeos viajaban principalmente a América y África siguiendo rutas no muy distantes del ecuador, y en estas latitudes la aproximación que ofrece la Mercator es muy buena ─aparte de otras ventajas que tiene a la hora de trazar rutas─. Sin embargo, cuando por el siglo XIX empezó a explorarse la Antártida y el Polo Norte, se observó que en tan altas latitudes los mapas con esta proyección no servían ni para limpiarse el culo.
Además, este comportamiento cerca de los polos explica otra de las afirmaciones que mencionaba al principio: por qué los países del hemiferio norte aparecen en general más grandes que los del sur. No es por ninguna pérfida manipulación, sino por el mero hecho de que en el hemisferio sur los países habitados tienden a estar apelotonados cerca del ecuador, mientras que en el norte llegan hasta mucho más cerca del polo. Así pues, se muestra Groenlandia más grande que Australia porque aquélla se encuentra por el paralelo 65 mientras que ésta sólo por el 35.
A lo anterior hay que unirle que, por cuestiones de ahorro y comodidad, y puesto a que se encuentra deshabitado, se tiende a eliminar de los mapas la única extensión de tierra del hemisferio sur que se encuentra cerca ─y tan cerca─ del polo: la Antártida. De hecho, si se incluyera la Antártida, aparecería con un tamaño desmedido, como se aprecia en la siguiente imagen:
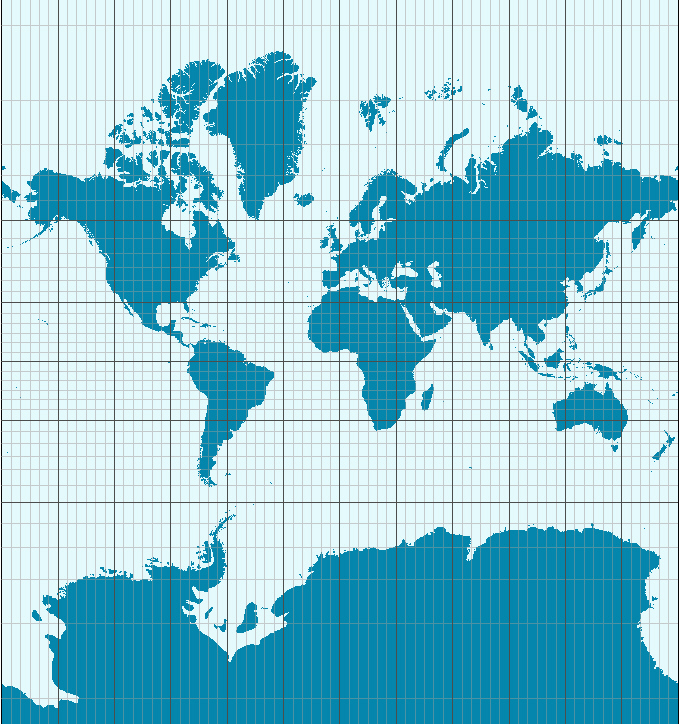
Para acabar, sólo quería mencionar de pasada que las proyecciones que he mencionado hasta ahora son cilíndricas, esto es, que son proyecciones de la esfera sobre un cilindro. Pero hay de los siguientes tipos en función de la superficie sobre la que se proyectan:
─ Cilíndricas
─ Cónicas
─ Azimutales
─ Modificadas
Para más información os remito a vuestro buscador favorito. En la wikipedia por ejemplo viene bastante bien explicado ─como de costumbre,
mejor en la inglesa que en la española─.
__________________________________________________________________________
(1) Se llama proyección a la forma en que se representa la superficie de una esfera en un plano.
(2) Para más información, ver el
Teorema Egregio de Gauss.
(3) En realidad debería conservar una propiedad relacionada a la forma pero más débil llamada
conformidad, pero para simplificar lo dejo así.






